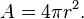How do we find the Volume of pyramids and cones?

To find the volume of a pyramid  ;
V= (1/3)B*H  



Volume of a cone ;
V=(1/3) πr²h  OR V= (1/3)BH

How do you find the Surface Area and Volume of a sphere?

To find the Surface Area of a sphere you would have to use this formula ;    



To find the Volume of  Sphere you would use this formula ;  


Find the surface area and area ;

how do we calculate Surface Area of a Cylinder?

 •To find the Surface Area of a cylinder you would use the formula
                                                             S.A.= L.A. + 2B

•To find Lateral Area ( L.A.) you would use the formula
                                                               L.A.= 2πrh

•One you get the lateral area you plug that number into the SA formula. The next step, you would have to find the area base of the base to plug it into the SA formula.
                                       Area of base= πr²

How do we identify Solids?

Solid Geometry
- Is the 3- dimensional space.
- There is 3 dimensions, width, depth, and height.



Solids of Properties
- Volume
- Surface Area (SA)

Types of Solids
- Polyhedra
- Non - Polyhedra

• Polyhedra: must have flat faces. Some shapes that are considered polyhedra are prisms, pyramids, and platonic solids.

• Non - Polyhedra: Only surfaces that are not flat. Shapes that are non-polyhedra are spheres, cylinders, cone, and torus. 

How do we find the area of a circle?

To find the area of a circle you would use the formula :
           
                 A =πr<sup>2
                       A is the area
                       r is the radius of the circle

WIth the given information you plug in the number(s) to the formula.</sup>

How do we find the area of regular polygons?

To calculate the area of a regular polygon you would use the formula :
                    A = ½ * nas        OR       A= ½ * Pa

A is the area
P is the perimeter
a is the apothem
s is the length of each side
n is the number of sides

how do we find the area of parallelograms, kites, and trapezoids?

When solving the area to a figure like parallelograms, kites,and trapezoids, each one of those shapes has their own formula.



  Area of a Parallelogram:

                                                                   

 Area of a Kite:

                                                                                         

 Area of a Trapezoid:                                                                                                                              

                                                        

                             

   

 Example #1                                                                                                                

                                                    

Parallelogram Area = B x H          

                                                            Area = 12  x 5                                             

                                                                         Area =  60 cm ²                                                        

Example #2                                                                                                             

                                    

                      Kite Area =  ½ d₁d₂

                                                                                                                        Area= ½ ( 8 x 6)                                                  

                             Area= ½  (48) 

                             Area = 24 cm ²

Example #3                                                                                                              

                               

Trapezoid Area = ½ h( b_{1 +}b₂ )

                     Area =  ½ 5(10 + 14)

              Area  =  ½ (120)

          Area  = 60in²
  

How do we calculate the area of rectangles and triangles?

Area- The total amount of units inside of a figure / shape.


When trying to solve the area of a triangle and a rectangle theres a formula to each shape.

 

 

Formula of a Triangle: 

Formula of a Rectangle:

Example #1:                                                                                    

Find the area of a triangle with base of 5in. and the height of  8in. 

        A= ½b × h
     A=½ (5) × (8)
     A= ½ × 40
     A= 20 in²

 Example #2:
Find the area of a rectangle with a base of 2cm. and height of 9cm.
    A= b × h
    A= (2)×(9)
    A= 18 cm²

How do we solve compound loci problems ?

When solving a compound locus problem, always involves two or more locus conditions in the same problem.

To know that there are more that one locus condition you would be able to identify it by seeing each one seperated by the words " AND " or " AND ALSO" 

To solve the two or more, locus conditions in the same problem you have to  solve each one seperately but on the same graph diagram.

How do we find the locus of points?

• A locus is a general graph of a given equation
• The locus is the set of all points that makes all the other points the same to the given condition
• There are 5 different locus

1. The locus of points equidistant ( the equal distance from another point)
        from a single point.

• Using the origin and forming a circle at the same distant all around the center( origin)

                      The locus of 1 unit from point A.

2. The locus of points equidistant from two fixed points.

• Forming a line through the middle of the two points

                                                    The locus of points P and Q is :

   

3. The locus of points from a single line.

• Two parallel lines would be equidistant formed on opposite side from the original line

4. Locus of points equidistant from two parallel lines.

• a line would be through the middle of the two lines.

5. The locus of points from two intersecting lines.

• two intersecting lines halfway between the two original lines.

How do we solve logic problems using conditionals?

When making a conditional there is a rule we have to remember
which is ,
            *   If hypotenuse then conclusion
Example:
            * If  the light is red, then the car will stop
                  
                 * If it is not raining, then i will take my umbrella


When sovling the conditional to a inverse you have to,
           * if not hypotenuse then not conclusion. 
Example:
            * conditional- if i walk all day then i am tired
             * inverse- if i do not walk all day then i am not tired 



Solving a conditional to a converse,
             *switch the hypotenuse and the conclusion.
Example:
            * conditional - if i walk all day then i am tired
            * inverse- if i am tired then i walk all day


Solving a conditional to a contrapositive (logical equivalent) follow this rule,
            * if not conclusion then not Hypotenuse
Example:
          * concditional- if i walk all day then i am tired
          * contrapositive- if i am not tired, then i did not walk all day

what is a mathematical statement?

 what is a mathematical statement?


A mathematical statement is a statement that can be proven true or false.
This probably a everyday thing.

An example of a mathematical statement would be;
The principle of CPEHS is Mr. Lieberman and a teacher in CPEHS is Mr. Schnatterly.
** THE WORD AND SHOWS THAT THIS STATEMENT MUST BE TRUE FOR THE STATEMENT TO BE TRUE.


There are 4 different statements that can be formed ;
    - the conditional
    - inverse
    - converse
    - contrapositive or logical equivalent

The conditional;
If I use a pink pen, then I am lucky.

The inverse;
If I am not using a pink pen, then I am not lucky, .

The converse ;
If I am lucky, then I am using a pink pen.

The comtrapositive;
If I am not lucky, then I am not using a pink pen.

How do we graph Rotations?

1. Know the angle of rotation.
2. Know the direction (either it is clockwise or counterclockwise)
3. Use the formula of the given angle to each point.

90 degree rotation
(x,y) → (-y,x)

-90 degree rotation
(x,y) → (-y,x)

180 degree rotation
(x,y) → (-x,-y)

270 degree rotation
(x,y) → (y,-x)

How do we use the other definitions of transformations?

Glide reflection- its a reflection of a figure in a lince and a translation along that line.

Orientaion- The arrangments of points.


Isometry-  When the image of the LENGTH and the SIZE stays the same after the transformation to the original shape.

Direct Isometry- when the orientaion of the letters stay the same and it's length.

Opposite Isometry- The letter points of the shape, is backwards on the image but the length are the same. Just like a reflection.

How do we graph dilations?

- Dilation is one of the four transformations that causes an image to stretch or shrinks using it's scale factor, to it's original size. * The description of A dilation usually includes the scale factor Or the ratio. * With the scale factor, you have to multiply the dimensions of the original To get the answer of the dilated image.

How do we identify transformations ?

A transformation is when you move a geometric figure. Including translation, rotation, reflection, and dialtion. 

• Translation- Every point is moved the same distance in the same direction.
• Reflection- figure is flipped over a line of symmetry.
• Rotation- Figure is turned around in one point.
• Dialtion- An enlargment or reduction in size of the image.